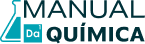Balancear uma equação química significa acertar os coeficientes estequiométricos (menores números inteiros e positivos que aparecem antes das substâncias nas equações) para que a quantidade de átomos de cada elemento seja igual nos dois lados da equação, isto é, nos reagentes (primeiro membro) e nos produtos (segundo membro).
Isso é importante primeiramente porque, conforme a Lei de Lavoisier da conservação das massas diz, “numa reação química feita em recipiente fechado, a soma das massas dos reagentes é igual à soma das massas dos produtos”. Atualmente, essa lei é mais conhecida como: “Na natureza, nada se perde, nada se cria, tudo se transforma.” Isso quer dizer que os átomos dos elementos nas reações não aparecem do nada e tampouco são destruídos. Mas, na verdade, esses átomos sofrem um rearranjo, “trocando de posições”, por assim dizer, pois as suas ligações anteriores são desfeitas e são formadas novas ligações químicas que dão origem aos produtos.
Portanto, o balanceamento das equações que representam as reações químicas é justamente tornar isso verdade. Além disso, é importante saber balancear as equações porque em processos químicos são realizadas análises e cálculos das quantidades de reagentes e/ou produtos (cálculos estequiométricos) em que se depende em grande parte do balanceamento das equações.
Um dos métodos mais utilizados para realizar o balanceamento das equações é o método das tentativas, que basicamente segue os seguintes passos:
1. Indicar o coeficiente “1” para o elemento que aparece em somente uma substância em um dos membros. Isso quer dizer que geralmente o hidrogênio e o oxigênio serão os elementos deixados para serem balanceados por último, respectivamente;
2. Quando mais de um elemento aparece somente uma vez em um dos membros, devemos escolher começar pelo que tiver maior quantidade de átomos. Isto é indicado pelo índice (número que aparece no canto inferior direito do elemento);
3. Prosseguir com os demais elementos. Para tal, é observada a quantidade de cada elemento que já existe em um dos membros e em seguida atribui-se um valor para o coeficiente desse elemento no outro membro, lembrando que ele deve ser multiplicado pelo índice resultando num valor que iguale à quantidade de átomos nos dois membros.
Por exemplo, considere a equação química que representa a reação de combustão do gás butano, que é um dos componentes do gás de cozinha:
C4H10(g) + O2(g) → CO2(g) + H2O(v)
Observe que no primeiro membro temos 4 carbonos, 10 hidrogênios e 2 oxigênios, enquanto que no segundo membro existe 1 carbono, 2 hidrogênios e 3 oxigênios. Então, sabemos que a equação não está balanceada. Vamos fazê-lo seguindo os passos mencionados anteriormente:
1. Observe nessa equação que o oxigênio aparece em duas substâncias no segundo membro e, portanto, não podemos começar o balanceamento por ele. O hidrogênio e o carbono aparecem somente em uma substância nos dois membros;
2. O carbono e o hidrogênio do butano são os que possuem mais átomos, por isso vamos começar por essa substância, atribuindo-lhe o índice “1”:
1 C4H10(g) + O2(g) → CO2(g) + H2O(v)
3. Agora sabemos que no primeiro membro existem 4 carbonos, então esse será seu coeficiente no segundo membro:
1 C4H10(g) + O2(g) → 4 CO2(g) + H2O(v)
Também sabemos que existem 10 átomos de hidrogênio no primeiro membro, então o coeficiente desse elemento no segundo membro será 5 (que é o número que multiplicado pelo índice 2 dará igual a 10):
1 C4H10(g) + O2(g) → 4 CO2(g) + 5 H2O(v)
Por fim, falta apenas o oxigênio. No segundo membro, temos 13 átomos de oxigênio (lembre-se de multiplicar os coeficientes pelos índices e depois somar tudo, assim: (4 . 2) + (5 . 1) = 13). Visto que no primeiro membro o índice do oxigênio é “2”, então, temos que o único número que multiplicado por 2 dá igual a 13 é 13/2:
1 C4H10(g) + 13/2 O2(g) → 4 CO2(g) + 5 H2O(v)
Na maioria dos balanceamentos terminaríamos aqui. No entanto, conforme mencionado no início, temos que encontrar os menores números inteiros e positivos, e no caso acima temos um número que não é inteiro, o 13/2. Então, para eliminar essa fração, multiplicamos todos os coeficientes (para não tirar a proporção estequiométrica) por 2:
2 C4H10(g) + 13 O2(g) → 8 CO2(g) + 10 H2O(v)
Pronto, a equação química está balanceada! Veja que em ambos os membros temos 8 carbonos, 20 hidrogênios e 26 oxigênios.
Existe também outra forma de realizar o método por tentativas, que é substituir os coeficientes por letras e fazer o seguinte esquema:
x C4H10(g) + y O2(g) → z CO2(g) + w H2O(v)
C = 4 x C = z
H = 10 x H = 2 w
O = 2 y O = 2 z + w
Então, começamos atribuindo o número 1 ao x e continuamos com as outras equações para descobrir os valores das outras letras, veja:
C = 4 x = 4 . 1 = 4
Como a quantidade de átomos de carbono no primeiro membro é igual a 4, então temos o seguinte no segundo membro:
C = z = 4
Agora vamos para o hidrogênio:
H = 10 x = 10 . 1 = 10
Visto que no primeiro membro a quantidade de átomos de hidrogênio é igual a 10, então temos o seguinte no segundo membro:
H = 2 w = 2 . 5 = 10
Por último, temos o oxigênio. Visto que não sabemos o valor de y, e já descobrimos que z = 4 e w = 5, então vamos resolver primeiro a sua equação que está no segundo membro:
O = 2 z + w
O = 2 . 4 + 5
O = 13
Agora, sabendo que tem que haver 13 oxigênios no primeiro membro, voltamos à outra equação:
O = 2 y = 2 . 13/2 = 13
Por fim, substituímos os valores encontrados para cada letra na equação química:
x C4H10(g) + y O2(g) → z CO2(g) + w H2O(v)
1 C4H10(g) + 13/2 O2(g) → 4 CO2(g) + 5 H2O(v) . (2)
2 C4H10(g) + 13 O2(g) → 8 CO2(g) + 10 H2O(v)
Esse é o mesmo que encontramos pelo método anterior.
Agora, aprenda a realizar o balanceamento de equações químicas que representam as reações de oxirredução no texto abaixo:
Balanceamento das equações de oxirredução.
Por Jennifer Fogaça
Graduada em Química
Videoaula relacionada:
