Modelo atômico de Schrödinger
O modelo atômico de Schrödinger descreve matematicamente o comportamento e a energia de partículas subatômicas, considerando a natureza corpuscular e ondulatória dos elétrons.
Por Everton da Paz Silva

PUBLICIDADE
O modelo atômico de Schrödinger é, na verdade, uma descrição matemática do comportamento e das energias de partículas submicroscópicas que considera a natureza corpuscular e ondulatória dos elétrons. Essa descrição foi desenvolvida pelo físico austríaco Erwin Schrödinger, em 1926, e representa uma evolução significativa no entendimento da estrutura atômica e no comportamento das partículas subatômicas. Diferente dos modelos anteriores, o modelo de Schrödinger introduziu uma abordagem mais profunda da Mecânica Quântica.
O principal avanço do modelo atômico de Schrödinger foi conseguir expressar em uma equação matemática, conhecida como equação de Schrödinger, o comportamento de partículas subatômicas, como os elétrons, em termos de uma função de onda. Essa nova visão propôs que os elétrons não seguem trajetórias fixas, mas ocupam regiões ao redor do núcleo onde há maior probabilidade de serem encontrados.
Esse conceito representou uma ruptura com a Física clássica, permitindo uma compreensão mais precisa das propriedades e das probabilidades associadas à localização e energia dos elétrons. Dessa forma, o modelo de Schrödinger não apenas reforçou a ideia de que os elétrons têm comportamentos ondulatórios, mas também ofereceu uma maneira de calcular, com precisão, a probabilidade de encontrar um elétron em determinada região do espaço, introduzindo o conceito de orbitais atômicos.
Leia também: Atomística — tudo o que você precisa saber sobre o estudo dos átomos
Resumo sobre o modelo atômico de Schrödinger
- O modelo atômico de Schrödinger é uma descrição matemática do comportamento e das energias de partículas submicroscópicas que considera a natureza corpuscular e ondulatória dos elétrons.
- Os estados de energia possíveis que um elétron pode assumir correspondem a funções de onda (\(\Psi\)) específicas que descrevem a probabilidade de o elétron ser encontrado ao redor do núcleo.
- A região do espaço onde existe a maior probabilidade de encontrar o elétron é definida como orbital.
- A equação de Schrödinger foi um marco na compreensão dos átomos, permitindo explicar com precisão os níveis de energia dos elétrons em átomos complexos.
- A estrutura do átomo e o entendimento de conceitos fundamentais que justificam a matéria e o seu comportamento foram explicados através de diferentes modelos atômicos.
Qual é o modelo atômico de Schrödinger?
O modelo atômico de Schrödinger é uma descrição matemática do comportamento e da energia de partículas subatômicas baseada na Mecânica Quântica. Essa teoria surgiu como resultado de avanços teóricos que mudaram a visão sobre o átomo e as partículas que o compõem, especialmente a dualidade de comportamento dos elétrons.
Em 1924, Louis de Broglie propôs o princípio da dualidade de partículas, que sugeria que o elétron poderia se comportar tanto como partícula quanto como onda. Esse princípio surgiu para explicar por que os elétrons se limitavam a orbitar o núcleo atômico em distâncias fixas e quantizadas, ou seja, em níveis de energia específicos, como previa o modelo proposto por Bohr.
A ideia da dualidade de Broglie implicava que o elétron, além de apresentar massa e ocupar posição no espaço como uma partícula, poderia também ser descrito como uma onda. Segundo de Broglie, o elétron não se comportaria apenas como uma partícula localizada, mas como uma onda estacionária que se propaga ao redor do núcleo e que, dessa forma, seu comprimento de onda se ajustaria exatamente à circunferência da órbita.
Contudo, se o elétron fosse realmente uma onda, como seria possível localizar sua posição com precisão? O conceito de onda implica uma propagação que ocupa uma região no espaço, tornando difícil determinar um ponto exato. Para lidar com essa dificuldade, o físico alemão Werner Heisenberg formulou o princípio da incerteza. Esse princípio afirma que é impossível determinar simultaneamente, com precisão absoluta, a posição e a velocidade (ou o momento linear) de uma partícula.
Em outras palavras, quanto mais precisamente tentamos medir a posição de um elétron, menos precisamente conseguimos determinar sua velocidade, e vice-versa. Esse princípio da incerteza trouxe uma nova perspectiva ao estudo das partículas subatômicas, aceitando que as limitações na medição são inerentes à própria natureza dos elétrons e demais partículas quânticas.
Assim, ao desenvolver seu modelo, Schrödinger utilizou uma abordagem que combinava o comportamento corpuscular e ondulatório dos elétrons. A equação formulada por Schrödinger permite calcular uma função de onda, denotada pela letra grega \(\Psi\) (psi), que descreve o estado do elétron em um átomo.
A função de onda (\(\Psi\)) por si só não tem um significado físico direto, mas seu quadrado (\(\Psi^2\)) representa a probabilidade de encontrar o elétron em uma certa região ao redor do núcleo. Essa ideia de probabilidade é semelhante ao conceito da intensidade de uma onda luminosa: enquanto a função de onda descreve a oscilação, o quadrado de sua amplitude define a intensidade da luz.
Cada ponto indica a probabilidade de o elétron ser encontrado no espaço, e quanto mais próximo do núcleo atômico, maior é essa probabilidade, como mostra a imagem abaixo.
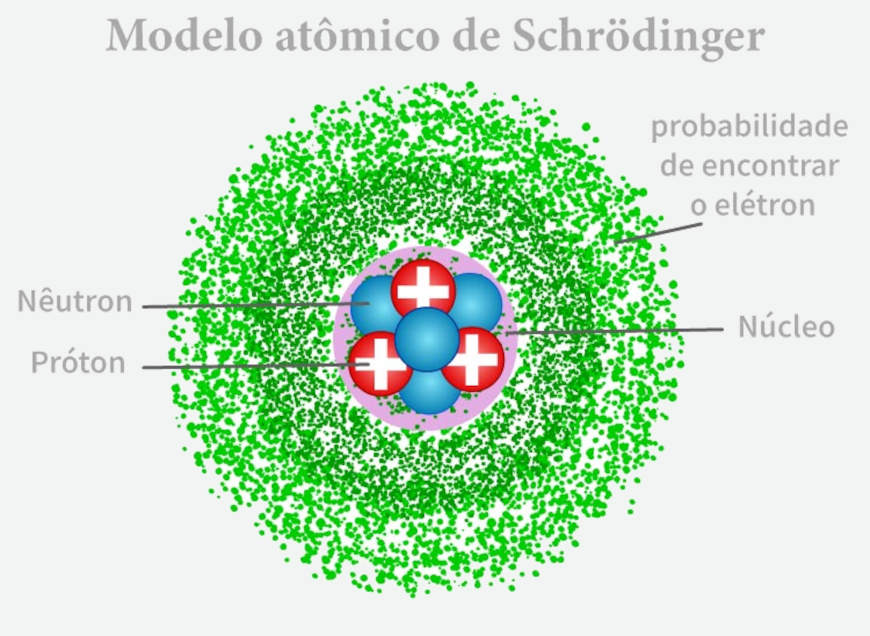
A equação de Schrödinger é expressa como:
\(-\frac{\hbar^2}{2m} \nabla^2\Psi + V\Psi = E\Psi \)
Nessa equação:
- \(\hbar\) é a constante reduzida de Planck;
- m representa a massa da partícula (nesse caso, o elétron);
- V é o potencial da região onde o elétron se encontra;
- E é a energia associada ao estado do elétron.
A presença do operador de Laplace \(\nabla^2\) indica que estamos lidando com uma função tridimensional, uma vez que o elétron se movimenta em três dimensões ao redor do núcleo.
A equação de Schrödinger pode ser expressa em uma forma simplificada para descrever partículas em campos de energia mais simples, como o caso de um elétron em um átomo de hidrogênio. Essa forma simplificada é conhecida como equação de Schrödinger independente do tempo e é utilizada quando se está interessado apenas nos estados estacionários, ou seja, estados de energia fixa da partícula.
A forma simplificada da equação de Schrödinger é dada por:
\(\hat{H} \Psi = E \Psi \)
Nessa expressão:
- \(\hat{H}\) é o operador hamiltoniano, que representa a energia total do sistema (a soma da energia cinética e da energia potencial);
- \(\Psi\)(psi) é a função de onda, que descreve o comportamento do elétron no espaço;
- E é o valor da energia associado ao estado descrito pela função de onda \(\Psi\).
Essa forma simplificada da equação de Schrödinger permite resolver problemas específicos em sistemas onde a energia não muda com o tempo, como o cálculo das órbitas eletrônicas em átomos. Ao aplicá-la, é possível encontrar as funções de onda \(\Psi\) e os níveis de energia E, que correspondem aos diferentes estados permitidos para os elétrons, como acontece nos níveis de energia do átomo de hidrogênio.
Veja também: O que dizia o modelo atômico de Rutherford-Bohr?
O que diz a teoria atômica de Schrödinger?
A equação de Schrödinger descreve como os elétrons se comportam em um átomo, especificando os estados de energia possíveis que um elétron pode assumir em um sistema simples, como o átomo de hidrogênio. Esses estados de energia são únicos e correspondem a funções de onda (\(\Psi\)) específicas que descrevem a probabilidade de o elétron ser encontrado ao redor do núcleo.
Esses estados de energia para o elétron, no átomo de hidrogênio, são caracterizados por um conjunto de números quânticos, que determinam as propriedades dos elétrons e, consequentemente, a configuração eletrônica e a estrutura atômica.
Como mencionado anteriormente, não é possível definir a região onde o elétron pode estar em um dado instante, mas é possível definir a probabilidade de encontrar o elétron em torno do núcleo (\(\Psi^2\)). Essa probabilidade de encontrar um elétron em uma região particular de um átomo é chamada de densidade eletrônica. Assim, quanto maior for a densidade eletrônica, maior é a probabilidade de encontrar o elétron em uma região do espaço. Essa região é chamada de orbital atômico e é definida pela função de onda de um elétron em um átomo.
A equação de Schrödinger descreve perfeitamente os estados de energia para o átomo de hidrogênio, que apresenta um único elétron ao redor de um único próton no núcleo. No entanto, em átomos que possuem mais de um elétron – conhecidos como átomos polieletrônicos – a equação de Schrödinger não pode ser resolvida exatamente. Isso ocorre porque a presença de múltiplos elétrons no átomo gera interações elétricas complexas, uma vez que cada elétron repele os demais devido à força eletrostática.
Essas interações de repulsão entre elétrons tornam o sistema muito mais complexo do que o caso de um único elétron orbitando ao redor de um núcleo. Para contornar esse desafio, são feitas aproximações do comportamento do átomo de hidrogênio, considerando que essa diferença não é muito grande.
Características do modelo atômico de Schrödinger
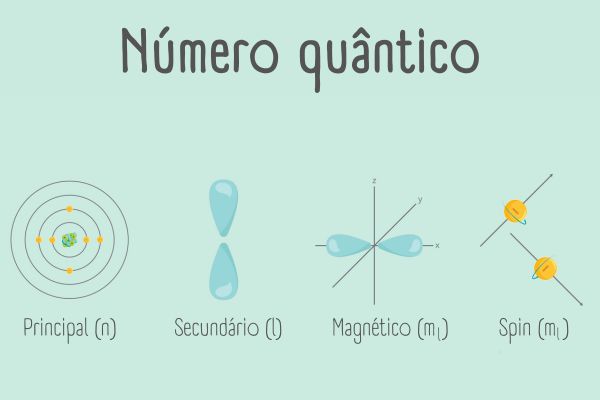
O modelo atômico de Schrödinger descreve a distribuição dos elétrons ao redor do núcleo dos átomos utilizando através de três números quânticos:
- número quântico principal (n);
- número quântico de momento angular (\(\ell \));
- número quântico magnético (\(m_\ell \)).
Cada um desses números quânticos representa características específicas dos orbitais atômicos e é usado para identificar os elétrons que ocupam as regiões ao redor do núcleo.
→ Número quântico principal (n)
O número quântico principal (n) é um valor inteiro (1, 2, 3, …) que indica a camada principal em que o elétron está localizado, e está relacionado com a distância média entre o elétron e o núcleo. Quanto maior o valor de n, maior será essa distância, o que implica que o elétron se encontra em um nível de energia mais alto e mais afastado do núcleo. Esse número quântico é crucial para a descrição da energia de um elétron em um átomo, pois reflete a sua posição em camadas eletrônicas.
→ Número quântico de momento angular (\(\ell\))
O número quântico de momento angular (\(\ell\)), também chamado de número quântico secundário ou azimutal, descreve o formato do orbital atômico. O valor de ℓ depende do número quântico principal (n); e para cada valor de n, \(\ell\) pode assumir valores inteiros que vão de 0 até n−1.
Esse número quântico revela a forma do orbital em que o elétron se encontra, e diferentes valores de \(\ell\) correspondem a diferentes tipos de orbitais, com designações específicas. Cada valor de ℓ é associado a uma letra que representa o tipo de orbital:
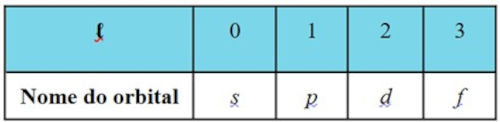
Essas designações de \(\ell\) permitem classificar os elétrons de acordo com o formato do orbital que eles ocupam, o que influencia diretamente as propriedades químicas do átomo. Assim, o número quântico de momento angular não apenas indica o formato dos orbitais, mas também define como os elétrons se distribuem em diferentes subníveis de energia dentro de cada camada principal.
→ Número quântico magnético (mℓ)
O número quântico magnético (\(m_\ell\)) descreve a orientação espacial do orbital atômico e depende do valor do número quântico de momento angular (\(\ell\)). Para cada valor específico de \(\ell\), há \(2\ell +1\) valores de \(m_\ell\). O número quântico magnético define o número de orientações possíveis para um orbital em um determinado subnível. Isso significa que para cada subnível de um dado valor de \(\ell\), temos um número definido de orbitais, cada um com uma orientação específica no espaço, como mostra a imagem a seguir.
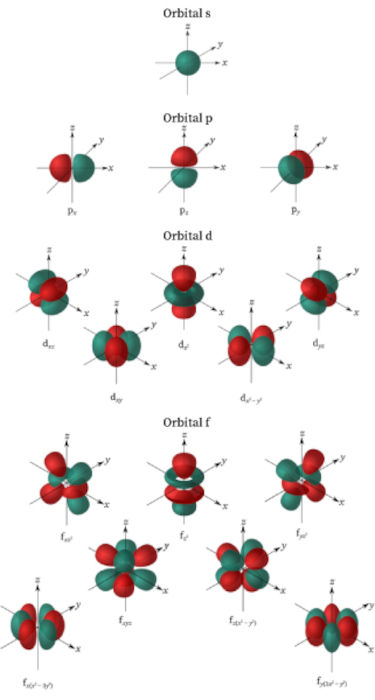
Esses orbitais podem acomodar elétrons, e a orientação deles influencia como os átomos se ligam a outros átomos, determinando a direção das ligações químicas.
Avanços do modelo atômico de Schrödinger em relação aos outros modelos atômicos
A teoria desenvolvida por Erwin Schrödinger foi um marco na compreensão dos átomos, permitindo explicar com precisão os níveis de energia dos elétrons em átomos complexos. Diferente do modelo de Bohr, que descrevia órbitas fixas para os elétrons e só era válido para o átomo de hidrogênio, o modelo de Schrödinger foi capaz de justificar os estados de energia de átomos com múltiplos elétrons, considerando as interações entre eles.
A inclusão de fatores como as forças de repulsão entre elétrons foi um avanço significativo, pois possibilitou um tratamento mais completo e realista das partículas subatômicas. Esse parâmetro, que foi incorporado à equação de Schrödinger, ajudou a tornar o modelo aplicável a átomos mais complexos do que o hidrogênio, o que era uma limitação do modelo de Bohr.
Além disso, o modelo de Schrödinger integra conceitos fundamentais da Mecânica Quântica, como o princípio da dualidade, que descreve o elétron como uma entidade com comportamento de partícula e onda, e o princípio da incerteza de Heisenberg, que impede a determinação simultânea e exata da posição e da velocidade de uma partícula. Dessa forma, o modelo de Schrödinger trouxe uma compreensão mais precisa da estrutura atômica, estabelecendo as bases para a moderna Química Quântica.
Os modelos atômicos
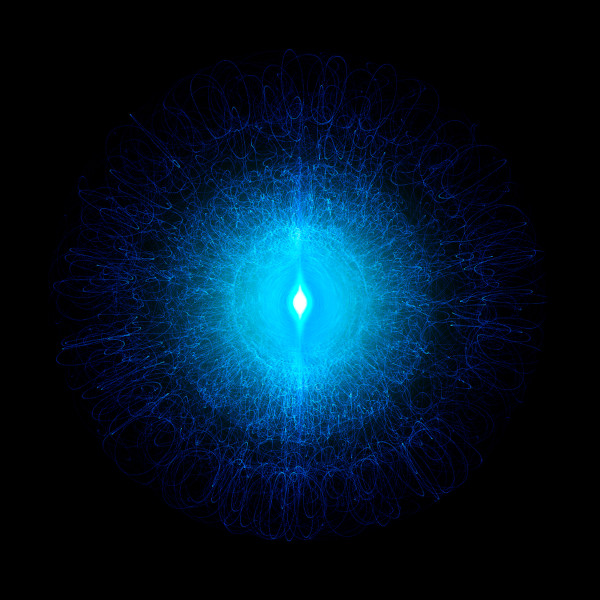
O conhecimento sobre a estrutura do átomo passa pelo desenvolvimento de conceitos fundamentais que justificam a matéria e o seu comportamento que foram explicados através de diferentes modelos atômicos.
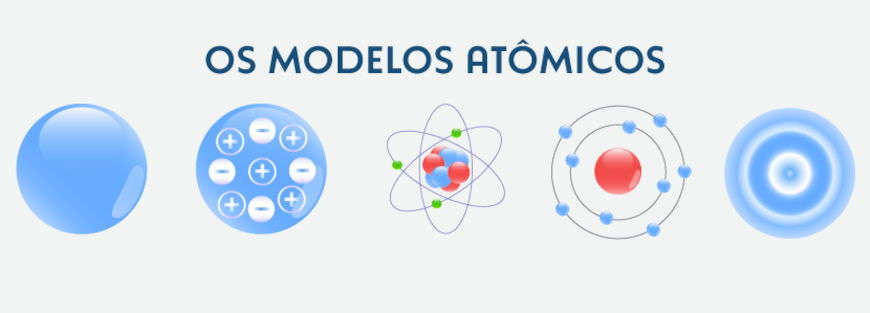
Cada modelo trouxe contribuições importantes para esse entendimento, como descritos a seguir.
- Modelo de Dalton: em 1808, John Dalton propôs que o átomo era uma partícula indivisível e indestrutível, semelhante a uma esfera maciça, sendo a menor unidade de matéria. Dalton introduziu o conceito de elemento químico, que é fundamental até os dias de hoje. Para saber mais sobre esse modelo atômico, clique aqui.
- Modelo de Thomson: em 1897, Joseph John Thomson descobriu o elétron e propôs o modelo do "pudim de passas", em que o átomo era uma esfera carregada positivamente com elétrons incrustados como passas em um pudim. Saiba mais clicando aqui.
- Modelo de Rutherford: em 1911, Ernest Rutherford, através do experimento da lâmina de ouro, propôs que o átomo possui um núcleo central pequeno e denso, carregado positivamente, com os elétrons ao seu redor, orbitando como planetas ao redor do sol. Para saber mais sobre esse modelo atômico, clique aqui.
- Modelo de Bohr: em 1913, Niels Bohr introduziu a ideia de níveis de energia quantizados, nos quais os elétrons orbitavam em órbitas fixas ao redor do núcleo, liberando ou absorvendo energia ao saltar entre essas órbitas.
- Modelo de Schrödinger: em 1926, Erwin Schrödinger desenvolveu uma descrição matemática dos elétrons em torno do núcleo, baseada na Mecânica Quântica. Em vez de órbitas fixas, ele propôs orbitais como regiões de alta probabilidade de localização do elétron, integrando conceitos como dualidade onda-partícula e o princípio da incerteza.
Esses modelos pavimentaram o caminho para a compreensão da estrutura atômica moderna.
Saiba mais: Quais são as propriedades da matéria?
Exercícios sobre modelo atômico de Schrödinger
1. O modelo atômico de Schrödinger representa um avanço significativo no entendimento da estrutura atômica. Uma das principais contribuições desse modelo é a definição dos chamados "orbitais atômicos", regiões de alta probabilidade de localização dos elétrons.
Com base no modelo de Schrödinger, assinale a alternativa correta:
A) O modelo de Schrödinger descreve o elétron como uma partícula em órbitas circulares fixas ao redor do núcleo, assim como o modelo de Bohr.
B) A equação de Schrödinger permite determinar, com exatidão, a posição e a velocidade de um elétron em torno do núcleo.
C) No modelo de Schrödinger, o conceito de orbital é substituído pelo de órbitas circulares, onde o elétron gira ao redor do núcleo.
D) Os orbitais atômicos descritos pelo modelo de Schrödinger representam regiões no espaço onde é máxima a probabilidade de encontrar o elétron.
E) O modelo de Schrödinger não utiliza conceitos da Mecânica Quântica e é baseado exclusivamente em observações experimentais.
Resolução: Alternativa correta: D.
Comentário: No modelo de Schrödinger, os orbitais atômicos são regiões do espaço ao redor do núcleo onde há uma alta probabilidade de encontrar o elétron. Diferente do modelo de Bohr, que utiliza órbitas fixas, o modelo de Schrödinger descreve uma distribuição probabilística, sendo essa uma de suas principais inovações. As alternativas A e C estão incorretas, pois a ideia de órbitas fixas é abandonada em favor dos orbitais. A alternativa B está errada porque o princípio da incerteza de Heisenberg afirma que não é possível determinar simultaneamente a posição e a velocidade de um elétron com precisão. A alternativa E está incorreta porque o modelo de Schrödinger se fundamenta na Mecânica Quântica.
2. A partir da equação de Schrödinger, foi possível descrever o comportamento dos elétrons em átomos, introduzindo a noção de números quânticos que especificam os orbitais. Os números quânticos fornecem informações sobre as características dos orbitais, como seu tamanho, forma e orientação no espaço.
Qual das alternativas abaixo descreve corretamente o significado dos números quânticos no modelo de Schrödinger?
A) O número quântico principal (n) representa a forma do orbital e depende dos valores de \(\ell\) e \(m_\ell\).
B) O número quântico de momento angular (\(\ell\)) determina o tamanho do orbital e está diretamente relacionado ao nível de energia.
C) O número quântico magnético (\(m_\ell\)) especifica a orientação do orbital no espaço, dependendo do valor de \(\ell\).
D) O número quântico principal (n) é responsável por definir a orientação espacial do orbital.
E) O número quântico magnético (\(m_\ell\)) indica a distância média do elétron em relação ao núcleo.
Resolução: Alternativa correta: C
Comentário: No modelo de Schrödinger, o número quântico principal (n) indica o nível de energia do elétron e está relacionado ao tamanho do orbital. O número quântico de momento angular (\(\ell\)) define a forma do orbital, enquanto o número quântico magnético (\(m_\ell\)) define a orientação do orbital no espaço, dependendo do valor de \(\ell\).
A alternativa C está correta porque descreve corretamente a função do número quântico magnético.
As alternativas A e D estão incorretas, pois o número quântico principal (n) não descreve a forma nem a orientação do orbital.
A alternativa B está incorreta, pois o número quântico de momento angular (\(\ell\)) não determina o tamanho do orbital. A alternativa E está errada porque \(m_\ell\) não define a distância do elétron ao núcleo.
Fontes
BROWN, Theodore L. et al. Química: a ciência central. 9.ed. São Paulo: Prentice Hall, 2005.
CHANG, Raymond. Química Geral: Conceitos Essenciais. 4ªed. São Paulo; McGraw-Hill, 2007.