Números quânticos

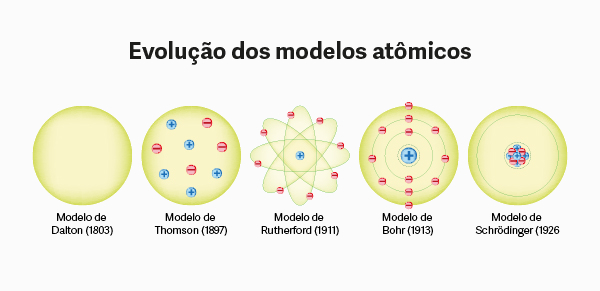
Os números quânticos são um conjunto de valores utilizados para descrever a energia e outras propriedades dos orbitais atômicos, os quais são regiões de probabilidade de existência de elétrons em torno do núcleo. Os números quânticos trazem informações não só sobre a energia dos elétrons, mas também acerca da forma dos orbitais atômicos e do momento angular deles.

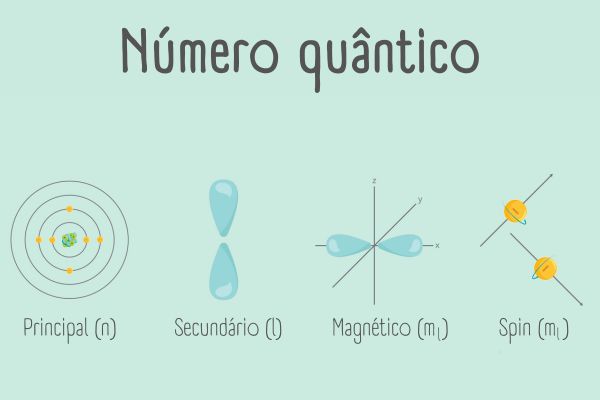
Os números quânticos para descrição de um orbital atômico são três (principal, secundário e magnético). Entretanto, existe um quarto número quântico, referente apenas à energia do elétron isolado, conhecido como número spin.  A compreensão dos números quânticos é essencial para a distribuição dos elétrons em torno do núcleo, bem como para diferenciá-los quanto à energia.

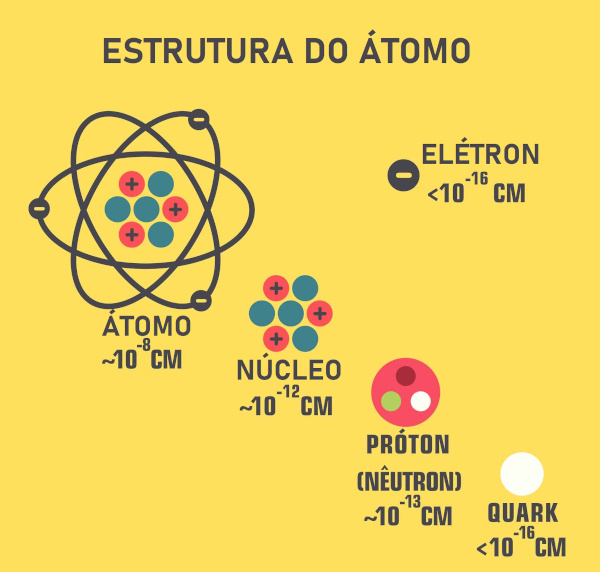
Leia também: Estrutura, representação e características do átomo

Resumo sobre números quânticos

• Os números quânticos são um conjunto de valores utilizados para descrição da energia dos orbitais atômicos, bem como outras propriedades, como tamanho e momento angular.
• Os orbitais atômicos são regiões de probabilidade de existência de um elétron em torno de um núcleo atômico.
• Três números atômicos descrevem um orbital atômico em um átomo tridimensional: principal, secundário e magnético.
  1. O número quântico principal descreve a energia total do orbital, bem como seu tamanho.
  2. O número quântico secundário descreve a sua forma e seu momento angular.
  3. O número quântico magnético distingue orbitais diferentes em uma mesma subcamada e apresenta a orientação rotacional do elétron.
• Há um quarto número atômico, o spin, que é específico do elétron de forma isolada. Ele descreve a rotação do elétron em torno de seu próprio eixo.

Videoaula sobre números quânticos

O que são números quânticos?

Os números quânticos são um conjunto de valores utilizados para descrever a energia e outras propriedades dos orbitais atômicos.

Em mecânica quântica, dadas as propriedades de onda dos elétrons, utilizamos as funções de onda para determinar a localização e as propriedades do elétron no átomo. Por exemplo, o quadrado da função de onda nos dá, segundo a interpretação de Max Born, um valor proporcional à probabilidade de se encontrar o elétron no átomo (densidade de probabilidade). Complementarmente, as funções de onda que descrevem a distribuição de um elétron em um átomo são chamadas de orbitais atômicos e são encontradas com a solução da equação de Schrödinger para o elétron.

Estando o elétron atraído ao núcleo em um átomo, podemos dizer então que existem limitações para a resolução da equação de Schrödinger nesse caso, ou seja, é necessário fazer ajustes na equação para concordar com o confinamento do elétron nesse sistema (o elétron está dentro de um átomo como uma partícula dentro de uma caixa). Como consequência, os resultados mostram que a energia de um elétron dentro de um átomo é quantizada, ou seja, um elétron só pode ter níveis específicos de energia por conta das especificidades do confinamento no átomo. Afinal, como existem limitações, existem situações específicas que não se adequam às especificidades do confinamento do átomo e, portanto, seriam entendidas como resoluções inadequadas da equação de Schrödinger (um paralelo para entender: imagine que você encontre um valor negativo para a velocidade de um objeto; isto, apesar de ser matematicamente possível, não é fisicamente correto, pois as condições de contorno não admitem velocidade negativa).

A resolução da equação de Schrödinger, por conseguinte, revela os níveis de energia permitidos para cada orbital atômico do elétron dentro de um átomo. Tais níveis distintos são descritos por um número quântico, chamado de principal, que não só representará o orbital atômico, mas também apresentará o seu tamanho e sua energia total. Se o átomo fosse unidimensional, apenas esse número seria necessário para descrever a energia do elétron, já que a energia é proporcional à distância do elétron em relação ao núcleo (ou seja, o tamanho do orbital atômico).

Porém, para um átomo tridimensional, outros números quânticos são necessários para descrever um orbital atômico, pois não só sua energia total deve ser interpretada, mas também sua forma e orientação no espaço. Assim sendo, números quânticos são essenciais para descrever o estado e as propriedades de uma partícula.

Para que servem os números quânticos?

A probabilidade de encontrar um elétron em um átomo é dada pelo seu orbital atômico, uma consequência da quantização da energia. A absorção de energia por um elétron faz com que ele mude o seu padrão de onda e, consequentemente, altere as características do orbital atômico.

Sendo assim, os números quânticos são utilizados para descrever o padrão de onda (o orbital atômico) do elétron dentro do átomo. Assim, podemos entender as diferenças de energia, tamanho, forma e a orientação espacial dos orbitais atômicos.

Leia também: Como é feita a distribuição eletrônica em orbitais

Quais são os números quânticos?

Um orbital atômico precisa de três números quânticos para defini-lo, os quais especificarão diferentes atributos:

• número quântico principal (n);
• número quântico secundário ou momento angular (l);
• número quântico magnético (m_l)

Há um quarto número quântico que não define o orbital, mas está associado ao momento magnético do elétron, conhecido como número quântico spin (m_s)

• Número quântico principal

É representado pela letra “n” e possui a maior contribuição para a energia do orbital. Por isso, é dito que esse número quântico especifica a energia de um orbital atômico de um elétron.

Em um átomo de apenas um elétron, todos os orbitais atômicos com mesmo valor de “n” possuem a mesma energia (estão degenerados) e, por isso, dizemos que pertencem à mesma camada eletrônica do átomo.

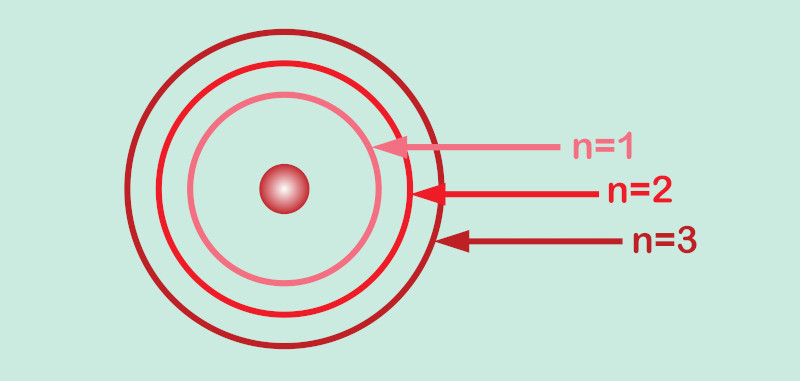
O número quântico principal também está associado ao tamanho do orbital atômico, pois, quanto maior o valor de “n”, maior se torna a região de máxima densidade de probabilidade de se encontrar o elétron; logo, a distância média entre o elétron e o núcleo aumenta com o incremento do valor de “n”.

O número quântico principal pode ser qualquer valor inteiro positivo (1, 2, 3...). O estado n = 1, o de mais baixa energia para um orbital atômico, é conhecido como o estado fundamental.

• Número quântico secundário, azimutal ou momento angular (l)

Representado pela letra “l”, tal número quântico está associado à forma do orbital. Seus valores podem ser l = 0, 1, 2, ...,  n−1.

Além disso, existem “n” valores diferentes de “l” para cada valor de “n”. Isso quer dizer que, para n = 2, podem existir dois valores diferentes para “l”, que são 0 e 1. O número quântico secundário apresenta o conceito de subcamadas (ou subníveis), diferenciando orbitais atômicos de mesmo “n”.

Por exemplo, para o nível energético n = 2, são possíveis dois valores diferentes para “l”, ou seja, são possíveis dois subníveis (l = 0 e l = 1). Para o nível 1, entretanto, só há um único subnível (l = 0). Isso nos leva a perceber que orbitais atômicos com número atômico “n” são divididos em “n” subníveis.

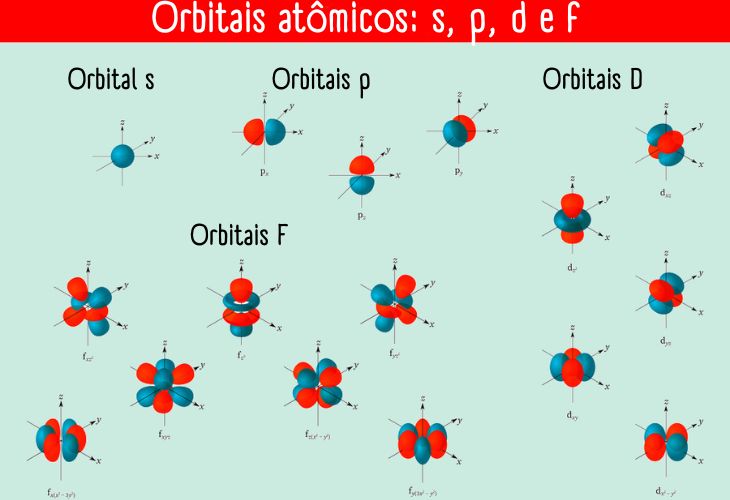
Os orbitais com diferentes valores de “l” recebem letras para identificá-los:

• orbital s (l = 0),
• orbital p (l = 1),
• orbital d (l = 2) e
• orbital f (l = 3).

De fato existe a possibilidade para l > 3 (dando origem aos orbitais g, h...), mas, na prática, só são utilizados os orbitais s, p, d e f.

O valor “l” apresenta também o momento angular do elétron no orbital, que pode ser entendido como a velocidade que o elétron “transita” (em termos de mecânica clássica) em torno do núcleo atômico. No caso do orbital s, em que l = 0, não devemos pensar que o elétron está com velocidade zerada em torno do núcleo (o que seria impossível para a mecânica quântica pelo princípio da incerteza de Heisenberg), mas igualmente distribuído em torno dele.

• Número quântico magnético (m_l)

Serve para distinguir os orbitais de uma mesma subcamada, apresentando os seguintes valores possíveis:

m_l = l, l−1; ...; −l

Existem “2l + 1” valores diferentes para m_l. Para um orbital p, em que l = 1, existem então três valores diferentes para o número quântico magnético (+1, 0 e −1). Contudo, elétrons que estão em orbitais de mesmo valor de “l” e diferentes valores de “m_l” são degenerados, mesmo em átomos com muitos elétrons.

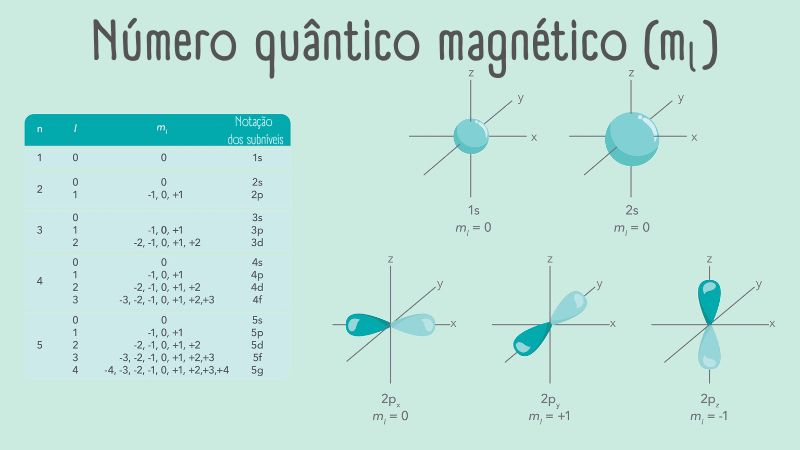
Esse número especifica a orientação do movimento orbital do elétron. Se, por exemplo, o valor de “m_l” é igual a +1, isso significa que o elétron possui um momento angular em torno de um eixo arbitrário; se o valor de “m_l” é igual a −1, o momento angular é o mesmo, mas em direção contrária em relação ao mesmo eixo arbitrário: por exemplo, em um caso,  o elétron “orbita” em sentido horário, enquanto no outro caso seria no sentido anti-horário. Para “m_l” igual a 0, a interpretação é semelhante para l = 0, ou seja, o elétron se distribui uniformemente ao redor de um determinado eixo arbitrário.

• Número quântico spin

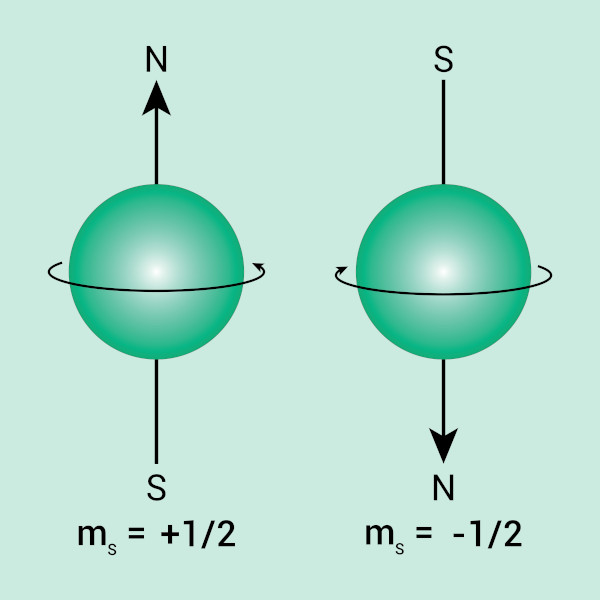
Mesmo com o rigor dos cálculos de Schrödinger, os valores apresentados ainda possuíam uma pequena distinção para o que era observado experimentalmente. Para fazer essa correção, dois físicos holandeses e naturalizados americanos, Samuel Goudsmit e George Uhlenbeck, propuseram a ideia de que os elétrons se comportariam como esferas em rotação em seu próprio eixo (como o planeta Terra, por exemplo). Tal propriedade seria conhecida como spin.

A mecânica quântica então admite dois estados de spin para os elétrons, representados por uma seta para cima (↑) e uma seta para baixo (↓), as quais indicam que o elétron pode rotacionar no sentido horário de seu eixo ou no sentido anti-horário de seu eixo. Para distinguir tais estados, criou-se o número quântico spin (m_s), que pode assumir os valores +½ (↑) e –½ (↓).

Exercícios resolvidos sobre números quânticos

Questão 1

(Unec Medicina/2022) Sabendo-se que a configuração eletrônica de um determinado elemento químico é [He]2s² 2p⁵ , é correto afirmar que os valores do número quântico principal e do secundário do elétron de valência deste elemento são, respectivamente,

a) 2 e 1

b) 2 e 2

c) 2 e 5

d) 5 e 1

e) 6 e 1

Resposta: Letra A,

O elétron de valência corresponde ao elétron de maior energia do subnível de maior energia do nível mais externo. Nesse caso, portanto, corresponde a um dos elétrons do orbital 2p, o qual possui número quântico principal (n) igual a 2 e número quântico secundário (l) igual a 1 (pois é subnível p).

Questão 2

(Urca 1º dia/2021.1) Os fogos de artifícios provocam um encantamento na maioria das pessoas, um verdadeiro show de luzes, formas e cores! As cores que observamos nos fogos de artifícios são obtidas quando são misturados a pólvora sais de elementos metálicos. A variedade de luzes coloridas observadas durante o espetáculo no céu depende do elemento químico presente nos sais. Sais de estrôncio (Sr) são responsáveis pela cor vermelha, sais de cobre (Cu) pela cor azul, sódio (Na) pelo amarelo, cálcio (Ca) pelo laranja e bário (Ba) pelo verde. Misturas de sais são usadas para as cores roxo (estrôncio e cobre), branco (magnésio, alumínio e titânio) e prata (magnésio e alumínio).

Qual o conjunto de números quânticos do último elétron do íon de cálcio no cloreto de cálcio, (considere spin do 1º elétron a entrar no orbital igual a − 1/2)?

Dado: Ca (Z=20).

a) n = 3; l = 1; m = +1; s = + 1/2.

b) n = 3; l = 1; m = +0; s = − 1/2.

c) n = 4; l = 0; m = 0; s = + 1/2.

d) n = 4; l = 0; m = 0; s = − 1/2.

e) n = 3; l = 2; m = −2; s = + 1/2.

Resposta: Letra A.

O cálcio, em sua forma iônica, sempre adquire a carga +2 (tem NOX fixo), portanto, no cloreto de cálcio (CaCl₂), está sob a forma de Ca²⁺.

Os dois elétrons retirados do átomo de cálcio para formar o íon cálcio devem ser da camada de valência do átomo de cálcio em seu estado fundamental. A distribuição eletrônica para o átomo de Ca (o qual possui 20 prótons e, sendo eletricamente neutro, possui 20 elétrons) é 1s² 2s²2p⁶ 3s²3p⁶ 4s². Assim, é possível perceber que a camada (ou nível) de valência é o orbital que possui n = 4 (pois esse é o mais externo).

Retirando-se dois elétrons da camada 4, esta deixa de existir e, por isso,  o íon Ca²⁺ possui a distribuição 1s² 2s²2p⁶ 3s²3p⁶.

O último elétron do íon cálcio está no subnível 3p, o qual possui n = 3 (3° nível) e l = 1 (pois é orbital p).

Como o orbital p possui três números quânticos magnéticos possíveis (-1, 0, +1), podemos dizer que os seis elétrons estão dipostos em pares com mesmo número quântico magnético, ou seja, há 2 elétrons com m_l = −1; 2 elétrons com m_l = 0 e 2 elétrons com m_l = +1. Esses elétrons de mesmo número quântico magnético, para evitarem repulsão, devem possuir spin contrário, então, por exemplo, um dos elétrons com m_l = −1 possui spin –½, enquanto o outro possui spin +½.

Pensando na distribuição dos elétrons dentro do orbital p, os três primeiros elétrons são dispostos com números quânticos magnéticos diferentes (um com −1, outro com 0 e outro com +1), a fim de diminuir as repulsões eletrônicas, mas sempre com o mesmo spin (segundo a questão, todos entram com spin –½). Os outros três elétrons são então distribuídos com números quânticos diferentes novamente, porém com spin contrário (+½).

Assim sendo, o último elétron a ser distribuído será aquele de m_l = +1 e spin = +½.

Fontes:

ATKINS, P.; JONES, L.; LAVERMAN, L. Príncípios de Química: Questionando a vida e o meio ambiente. 7. ed. Porto Alegre: Bookman, 2018.

MIESSLER, G. L.; FISCHER, P. J.; TARR, D. A. Química Inorgânica. 5. ed. Pearson Education do Brasil: São Paulo, 2014.